Nite
Nite

计算机和网络安全课程笔记 Week 2

Nite Nite 收录于 笔记 和 计算机和网络安全
 约 1500 字 预计阅读 7 分钟 

阅读 PDF

对称密码 (Symmetric Ciphers)

实现保密性的传统方式是通过共享一个秘密密钥 (secret key)。这也被称为对称加密 (symmetric encryption)，因为加密和解密消息使用的密钥是相同的。

对称密码由一个加密算法 $E_k$ 和一个解密算法 $D_k$ 组成，其中 $D_k$ 是 $E_k$ 的逆运算。也就是说，对于所有密钥 $k$ 和消息 $m$，有 $D_k(E_k(m)) = m$。

在对称密码系统中：

  1. Alice 和 Bob 共享：
    • 一个秘密密钥 $k$。
    • 一个加密算法 $E_k$。
    • 一个解密算法 $D_k$。
  2. Alice 想要发送消息 $m$ 给 Bob。未加密的消息称为明文 (plaintext) 或明文 (cleartext)。
  3. Alice 通过计算密文 (ciphertext) $c$ 来加密 $m$：$c = E_K(m)$。
  4. Bob 通过计算原始明文消息 $m$ 来解密 $c$：$D_k(c) = m$。

一个密码系统 (cryptosystem) 是一个包含算法以及所有可能的明文、密文和密钥的系统。

在没有秘密密钥 $k$ 的情况下，计算上困难 (computationally hard) 解密密文 $c$。秘密密钥 $k$ 通常是大量比特 (>= 128)。$k$ 可能值的范围称为密钥空间 (key space) $K$。可能消息的范围称为消息空间 (message space) $M$。

对于 128 比特的密钥，密钥空间 $K = {0, 1}^{128}$，即 ${0, 1, …, 2^{128}-1}$。

对称密码主要有两种类型：

  1. 流密码 (Stream Ciphers)：一次操作一个比特或字节。
  2. 分组密码 (Block Ciphers)：一次操作一块 (多个比特) 明文。

密码分析 (Cryptanalysis)

密码分析用于攻破密码安全系统 (breach cryptographic security systems)，并在即使不知道密码密钥的情况下，访问加密消息的内容。

我们总是假设攻击者拥有：

  1. 完全访问通信信道 (communications channel) 的权限。
  2. 完全了解密码系统 (cryptosystem)。

安全性只能依赖于密钥 (Secrecy must only depend on the key)。

密码分析攻击类型 (Cryptanalysis Attacks)

攻击类型按攻击者可获得的信息量从弱到强排序：

  1. 唯密文攻击 (Ciphertext Only Attack, COA)

    • 攻击者只拥有密文。
    • 已知 $c_1 = E_k(m_1), c_2 = E_k(m_2), …, c_n = E_k(m_n)$。
    • 目标是找到任何消息 $m_1, m_2, …, m_n$，秘密密钥 $k$，或者能够从 $c_j$ 推断出 $m_j$ 的算法。

  2. 已知明文攻击 (Known Plaintext Attack, KPA)

    • 攻击者截获了一些随机的明文/密文对 $(m, c)$。
    • 已知 $[m_1, c_1 = E_k(m_1)], [m_2, c_2 = E_k(m_2)], …, [m_n, c_n = E_k(m_n)]$。
    • 目标是找到秘密密钥 $k$，或者能够从 $c_j$ 推断出 $m_j$ 的算法。
    • 示例：攻击者知道加密的是源代码，开头很可能是 #include、版权声明等。

  3. 选择明文攻击 (Chosen Plaintext Attack, CPA)

    • 攻击者可以选择消息 $m$ 并获得对应的密文 $c$。
    • 已知 $[m_1, c_1 = E_k(m_1)], …, [m_n, c_n = E_k(m_n)]$ (其中 $m$ 是选择的)。
    • 目标是找到秘密密钥 $k$，或者能够从 $c_j$ 推断出 $m_j$ 的算法。
    • 比 KPA 更强。一些对 KPA 有抵抗力的密码对 CPA 则没有。

  4. 选择密文攻击 (Chosen Ciphertext Attack, CCA)

    • 攻击者可以指定密文 $c$ 并获得对应的明文消息 $m$。
    • 已知 $[c_1, m_1 = D_k(c_1)], …, [c_n, m_n = D_k(c_n)]$ (其中 $c$ 是选择的)。
    • 目标是找到秘密密钥 $k$。

破解等级 (Classes of Break)

从最差到最轻微的破解等级：

  1. 完全破解 (Total Break)：攻击者找到秘密密钥 $k$，因此可以计算所有解密消息 $D_k(c)$ 并执行加密 $E_k(m)$。
  2. 全局推导 (Global Deduction)：攻击者找到替代算法 $A$，等同于解密所有消息 $D_k(c)$ 而无需找到 $k$。
  3. 局部推导 (Local Deduction)：攻击者找到或解密一个截获密文的明文。
  4. 信息推导 (Information Deduction)：攻击者获得关于密钥或明文的一些信息，例如文件的前几个比特、消息的含义、文件类型等。

攻击度量 (Attack Metrics)

如果攻击者无论拥有多少密文，都没有足够的信息来推导出明文，那么该密码就是无条件安全 (unconditionally secure) 的。

信息安全是一场资源博弈，攻击的度量包括：

  1. 数据需求 (Data Requirements)：需要多少数据才能成功。
  2. 处理需求 (工作量) (Processing requirements (work factor))：执行攻击需要多少时间。
  3. 内存需求 (Memory requirements)：需要多少存储空间。
  4. 计算成本 (Computational cost)：需要多少 GPU 实例。

基本密码类型 (Basic Cipher Types)

替换密码 (Substitution Ciphers)

替换密码是最古老的密码形式。秘密密钥由一个明文和密文之间字母替换的表格组成。

  1. 最著名的是凯撒密码 (Caesar cipher)，每个字母偏移 3 位 (模 26)。
  2. 类似于 ROT13，它将明文移位 13 位。其最大优点是加密两次会得到原始明文：ROT13(ROT13($m$)) = $m$。
  3. 单表替换密码 (Monoalphabetic substitution cipher) 有 26! (阶乘) 种不同的可能密钥 (约 $2^{88}$ 或 88 比特)。
  4. 单表替换密码很容易被破解 (唯密文攻击)，利用字母的频率分析 (frequency analysis)：单字母 (Single letters)、二连体 (Digraphs) (字母对)、三连体 (Trigraphs) (三个字母)。

改进的替换密码：同音替换密码 (Homophonic Ciphers)

同音替换密码

同音替换密码是一种替换密码，它用多个符号替换一个常用字母 (例如，E 可以映射到 [C, ε, O])。

  1. 字母频率的峰或谷被隐藏起来，因为它们被分解成多个较小的峰。
  2. 字母“E” (英语中最常见的字母) 的高频率被分散到几个字符中，使得频率分析变得困难得多。

置换密码 (Permutation Ciphers)

置换密码也称为换位密码 (transposition ciphers)。秘密密钥 $\pi$ 是一个随机置换 (random permutation)。

  1. 给定消息 $m = [m_1, m_2, m_3, …, m_n]$。
  2. 加密计算为：$E_\pi(m) = [m_{\pi(1)}, m_{\pi(2)}, m_{\pi(3)}, …, m_{\pi(n)}]$。
  3. 如果 $\pi$ 是某个置换，例如将位置 1 映射到 3，位置 2 映射到 5，位置 3 映射到 2 等，那么 $E_\pi(\text{“crypto”}) = \text{“PYCTRO”}$ (示例置换见源文档)。

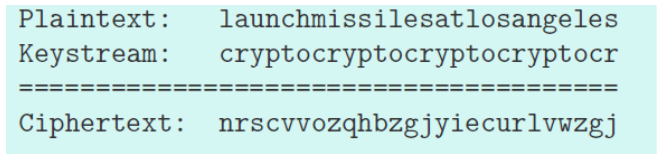
维吉尼亚密码 (Vigenere Cipher)

维吉尼亚密码

起源于 16 世纪的罗马。维吉尼亚密码是一种多表替换密码 (polyalphabetic substitution cipher)，由多个单表替换密码组成。

  1. 秘密密钥是一个重复的单词。
  2. 加密通过对密钥进行模 26 加法 (addition modulo 26) 来执行。
    • L + C = 11 + 2 = 13 mod 26 = 第 13 个字符 ⇒ N。
    • N + Y = 13 + 24 = 37 mod 26 = 第 11 个字符 ⇒ L。
    • 注意：A 是第 0 个字符。
  3. 标点符号和空格被移除以增加密码分析的难度。

破解维吉尼亚密码：重合指数 (Index of Coincidence, IC)

维吉尼亚密码可以使用重合指数 (index of coincidence) 与简单替换密码区分开来。

  1. 重合指数是一种统计度量，用于评估两个随机文本中相同位置出现相同字母的概率。
  2. 重合指数 $\kappa$ 的计算公式为： $$ \kappa = \frac{\sum_{i=A}^Z F_i(F_i-1)}{N(N-1)} $$ 其中，$F_i$ 是字母 $i$ (A, B, …, Z) 在密文中的计数，$N$ 是密文的长度。
  3. 对于使用英语标准频率的文本，重合指数的概率大约是 $K_p = 0.0667$。
  4. 如果文本是随机的，字母出现概率相等，那么重合指数的概率要小得多：$K_p = 0.0385$ (= 1/26)。

使用重合指数检测维吉尼亚密码的密钥长度：

  1. 将密文分成 $N$ 个切片 (slices)，方法是选取每 $N$ 个字母。然后计算这些切片的平均重合指数。
  2. 对不同的 $N$ 值重复此过程。
  3. 最可能 的密钥长度 $N$ 是使得平均重合指数最接近英语标准值 (0.0667) 的那个值。
  4. 一旦密钥长度 $N$ 已知，就可以独立攻击消息的 $N$ 个切片。密文的每个切片 $C_i$ 都是一个独立的单表替换密码。
  5. 注意：重合指数随语言而变化，并且可能特定于领域 (例如，物理期刊论文的重合指数可能明显不同)。

XOR 和一次性密码本 (One Time Pad, OTP)

XOR (异或)：

  1. XOR 是“互斥或”操作：一个或另一个，但不能两者都有。它是模 2 加法 (addition modulo 2)，用 $\oplus$ 表示：$a \oplus b = (a + b) \pmod 2$。
  2. 自己和自己异或得到零：$A \oplus A \equiv 0$。
  3. XOR 满足结合律 (associative)：$A \oplus (B \oplus C) \equiv (A \oplus B) \oplus C$。
  4. XOR 满足交换律 (commutative)：$A \oplus B \equiv B \oplus A$。
  5. XOR 常用于程序中提供安全性，本身非常弱，但构成了大多数密码原语的基础。
  6. 典型地，我们对比特进行 XOR 运算，将明文与密钥流 (key stream) 进行异或以生成密文。
  7. 这与维吉尼亚密码 (模 26 加法) 是一样的，只是 XOR 是模 2 加法，因为我们处理的是比特而不是字母。

XOR 加密：

  1. 消息 $m$ 按位与秘密密钥 $k$ 进行 XOR：
    • $c = m \oplus k$
    • $m = c \oplus k$
  2. 由于 XOR 实际上是维吉尼亚密码的一种，因此很容易破解：
    • 从重合指数确定密钥长度 $N$。
    • 将密文移位 $N$ 并与自身进行 XOR。
  3. 这会消除密钥 $c \oplus c’ = m \oplus k \oplus m’ \oplus k = m \oplus m’$。
  4. 结果是消息与自身移位版本进行了 XOR。语言具有极高的冗余性 (英语每字节约 1.3 比特信息)。然后很容易解密。

一次性密码本 (One Time Pad, OTP)：

  1. 一次性密码本是为明文的每个字母使用不同的替换密码。
  2. 一次性密码本是完美安全 (perfectly secure) 的，前提是：
    • 秘密密钥 $k$ 是真正随机的 (truly random)。
    • 明文不重复 (plaintext does not repeat)。
    • 密钥流不重复 (keystream does not repeat)。
  3. 未能满足上述任何一个要求都会导致零安全 (zero security)。
  4. 其强度来自于一个真正随机的密钥加到明文上会产生一个真正随机的密文。
  5. 任何计算能力都无法破解一次性密码本。暴力破解会产生该长度的每一个可能的明文。
  6. 核心问题：密钥分发 (key distribution)、密钥销毁 (key destruction)、同步 (synchronisation)。
  7. $k$ 的长度必须与 $m$ 相同。加密 1GB 数据需要 1GB 的共享密钥。
  8. 用于超安全、低带宽通信 (ultra-secure, low bandwidth communications)，例如军事卫星、莫斯科-华盛顿热线。
  9. 未来：量子密钥分发 (Quantum Key Distribution)，用于远距离安全分发密钥。

完美保密性 (Perfect Secrecy)

密码学的目标：密文不透露关于明文的任何信息。

  1. 如果对于所有 $m \in M, c \in C$，明文和密文在统计上是独立 (statistically independent) 的，则密码具有完美保密性： $$ \text{Pr}(\mathcal{M} = m | \mathcal{C} = c) = \text{Pr}(\mathcal{M} = m) $$
  2. 很少有密码拥有完美保密性。原因在于，在大多数密码中，密钥比消息短得多。

破解 OTP (Breaking OTP)

  1. 两次使用的密码本 (Two-Time Pad)：

    • 两次使用同一个密钥加密两个消息是完全不安全 (perfectly insecure) 的。
    • 假设两个消息 $m_1, m_2$ 使用同一个密钥 $k$ 加密：
      • $c_1 = m_1 \oplus k$
      • $c_2 = m_2 \oplus k$
    • 通过对密文进行 XOR 可以消除密钥：$c_1 \oplus c_2 = m_1 \oplus k \oplus m_2 \oplus k = m_1 \oplus m_2 \oplus k \oplus k = m_1 \oplus m_2$。
    • 由于英语和 ASCII 的冗余性，$m_1 \oplus m_2$ 通常很容易分离。

  2. 可塑性攻击 (Malleability Attack)：

    • OTP 和所有流密码都是高度可塑的 (highly malleable)。
    • 攻击者可以在不知道密钥的情况下，翻转密文中的比特，从而翻转明文中的对应比特。
    • 示例：如果明文是一个一位的投票 $v \in {0, 1}$ (0 代表 Labor，1 代表 Liberal)。Alice 使用 OTP 加密投票 $c = v \oplus k$ 并发送。Mallory 截获密文，翻转比特后发送 $c’ = c \oplus 1 = !c$。Bob 收到 $c’$ 并解密：$c’ \oplus k = c \oplus 1 \oplus k = v \oplus k \oplus 1 \oplus k = v \oplus 1 = !v$。攻击者成功改变了投票结果。

伪随机数生成器 (PRNGs) 和流密码 (Stream Ciphers)

伪随机数生成器 (Pseudorandom Number Generators, PRNGs)

在很多场合都需要随机数来源：会话密钥 (Session Keys)、洗牌、挑战 (Challenges)、Nonces (随机数)。

  1. 计算机本质上是确定性的 (deterministic)。因此，真正的随机性 (true randomness) 很难获得。
  2. 由于无法轻松获得真正的随机性，我们使用伪随机数生成器函数 (PRNGs) 来生成看起来统计上随机的输出序列。
  3. 密码学安全伪随机数生成器 (Cryptographically secure pseudo-random number generator, CSPRNG) 是一种 PRNG，其特性使其适用于密码学。

随机性的来源 (Sourcing Randomness)：

  1. PRNG 函数在提供特定的“种子”数据 (seed data) 时会产生相同的看起来随机的输出序列。
  2. 由于计算机是确定性的，它必须从外部的、真正随机的源提取随机性 (熵 - entropy)。这可能包括：硬盘驱动器的热噪声 (Thermal noise)、电压读数的低位波动 (Low-order bit fluctuations of voltage readings)、用户输入 (User input)、盖革计数器点击计时 (Geiger counter click timing)。
  3. 随机性实际上很难获得。

PRNG 的属性 (Properties of PRNGs)：

  1. 期望属性包括：
    • 可重复性 (Repeatability)
    • 统计随机性 (Statistical randomness)
    • 长周期/循环 (Long period/cycle)
    • 计算效率 (Computational efficiency)
  2. PRNGs 通常被以下方式破解：
    • 统计测试 (Statistical tests) 发现输出序列中的模式或偏差。
    • 从输出序列推断内部寄存器的状态 (Inferring the state of the internal registers)。
  3. PRNGs 在密码系统中通常至关重要。它们常常是单点故障 (single point of failure)。

特定的 PRNGs：

  1. 线性同余生成器 (Linear Congruential Generators, LCGs)：
    • 通过种子 $x_0$ 和规则 $x_{n+1} = (ax_n + b) \pmod c$ 生成序列 $x_1, x_2, …$。
    • 周期至多为 $c$。
    • 易受攻击 (Vulnerable)，因为只需要三个值 $x_i, x_{i+1}, x_{i+2}$ 就可以确定 $a$ 和 $b$。
    • 优点：简单快速实现，只需存储序列中最新的一个数，使用相同种子可以生成完全相同的序列 (对比较不同系统有用)。
  2. 线性反馈移位寄存器 (Linear Feedback Shift Registers, LFSRs)：
    • 简单地组合一系列寄存器的比特并将输出移入寄存器。
    • 种子是寄存器的初始值。
    • 在硬件中实现简单快速 (每个时钟周期 1 比特输出)。
    • 问题：抽头配置 (tap configuration) 可以从 $2n$ 个输出比特确定，其中 $n$ 是 LFSR 的周期长度。
  3. 其他 PRNG 示例：RC4 (基于 256 字节数组的置换)、ANSI X9.17 (基于 3DES)、DSA PRNG (基于 SHA 或 DES)、RSAREF PRNG (基于 MD5 散列和模 $2^{128}$ 加法)、Mersenne Twister (基于梅森素数 $2^{19937}-1$，是一种反馈移位寄存器，是最广泛使用的通用 PRNG)。

PRNG 漏洞和缓解 (PRNG Vulnerabilities)：

  1. 无法证明序列是真正随机的。
  2. 使用 PRNG 种子时要极其小心。
    • 使用时间戳或计数器对 PRNG 输入进行散列 (Hash PRNG inputs with a timestamp or counter)。
    • 偶尔重新播种 PRNG (Reseed the PRNG occasionally)。
    • 如果 PRNG 易受攻击，使用散列函数保护 PRNG 输出 (Use a hash function to protect PRNG outputs)。

PRNGs 用于流密码 (PRNGs for Stream Ciphers)

在一次性密码本中，我们有一个完美的随机串 $r$，其大小与消息 $m$ 相同，密文是 $c = r \oplus m$。

  1. 想法：用一个伪随机流 (pseudo-random stream) 替换 $r$。
  2. PRNG 的种子 (seed) 就是密钥 $k$。
  3. 加密：$E_k(m) = m \oplus \text{PRNG}(k)$。
  4. 解密：$D_k(c) = c \oplus \text{PRNG}(k)$。
  5. 当密钥 $k$ 被扩展成一个大的伪随机流时，这被称为流密码 (stream cipher)。

流密码 (Stream Ciphers)：

  1. 优点：
    • 易于实现和使用。
    • 安全的 PRNG 可以比分组密码快很多。
  2. 流密码的安全性直接取决于伪随机数生成器的安全性。
  3. 在计算上必须难以找到种子 $k$ 或序列 PRNG$(k)$。
  4. 种子 $k$ 必须只使用一次 (The seed k must be used only once)。
  5. PRNG 的周期必须至少与消息一样长。
  6. 与一次性密码本一样，流密码本身只确保保密性 (secrecy)。消息在传输过程中仍然可能被修改。

考点总结与示例考题

以下是一些可能作为考点的知识点，尤其注意加粗的部分。

可能考点

  1. 密码学的基本概念和目标 (安全通信、不安全信道、Eve 攻击者模型)。
  2. 密码学提供的安全服务 (认证、保密性、完整性、不可否认性)。
  3. 对称密码的定义和工作原理 (共享密钥、加密算法、解密算法、明文、密文，$D_k(E_k(m)) = m$)。
  4. 密码系统 (Cryptosystem) 的定义。
  5. 密钥空间 (Key space) 和密钥长度。理解大密钥空间带来的破解难度 (暴力破解)。
  6. 流密码 (Stream Ciphers) 和分组密码 (Block Ciphers) 的区别。
  7. 密码分析 (Cryptanalysis) 的目标和基本假设 (攻击者了解密码系统、安全性只依赖于密钥)。
  8. 主要的密码分析攻击类型：
    • 唯密文攻击 (COA)
    • 已知明文攻击 (KPA)
    • 选择明文攻击 (CPA)
    • 选择密文攻击 (CCA)
    • 理解它们之间攻击者能力的差异。
  9. 密码破解的等级：完全破解、全局推导、局部推导、信息推导，理解它们的严重程度排名。
  10. 衡量攻击的度量 (数据、处理、内存、计算成本)。
  11. 基本密码类型：
    • 替换密码 (Substitution ciphers) (单表替换、凯撒密码、ROT13)。
    • 单表替换密码的漏洞：频率分析。
    • 同音替换密码 (Homophonic Ciphers) 如何增强替换密码的安全性。
    • 置换密码 (Permutation Ciphers) 或换位密码 (Transposition ciphers) 的原理。
    • 维吉尼亚密码 (Vigenere Cipher) 的原理 (多表替换、重复密钥、模 26 加法)。
  12. 破解维吉尼亚密码的关键技术：
    • 重合指数 (Index of Coincidence, IC) 的定义和作用。
    • IC 的计算公式。
    • 如何使用 IC 确定维吉尼亚密码的密钥长度 (切片、计算平均 IC、与标准值比较)。
    • 确定密钥长度后如何破解 (每个切片视为单表替换)。
  13. XOR 运算：
    • XOR 的定义和基本属性 ($a \oplus b = (a+b) \pmod 2$, $A \oplus A = 0$，结合律，交换律)。
    • XOR 如何用于加密 ($c = m \oplus k$, $m = c \oplus k$)。
    • 为什么简单的 XOR 密码 (使用重复密钥) 易受攻击。
    • 如何破解重复密钥的 XOR 密码 (移位后异或消除密钥，$m \oplus m’$，利用语言冗余性)。
  14. 一次性密码本 (One Time Pad, OTP)：
    • OTP 的定义。
    • OTP 完美安全 (Perfectly secure) 的条件 (密钥真正随机、明文不重复、密钥流不重复)。
    • OTP 完美安全的原理 (随机密钥生成随机密文)。
    • OTP 的核心问题和缺点 (密钥长度与消息相同、密钥分发、密钥销毁、同步)。
  15. 完美保密性 (Perfect Secrecy) 的定义。理解为什么大多数密码无法实现完美保密性 (密钥比消息短)。
  16. OTP 的破解方式：
    • 两次使用的密码本 (Two-Time Pad) 攻击 ($c_1 \oplus c_2 = m_1 \oplus m_2$，如何利用语言冗余性破解)。
    • 可塑性攻击 (Malleability Attack) (攻击者如何在不知道密钥的情况下修改明文，示例：翻转投票)。
  17. 伪随机数生成器 (PRNGs)：
    • 为什么需要 PRNGs (计算机确定性，难以获得真随机性)。
    • PRNG vs CSPRNG。
    • 种子 (seed) 的作用和随机性来源 (熵)。
    • PRNG 的期望属性 (可重复性、统计随机性、长周期、效率)。
    • PRNG 的常见漏洞 (统计测试、推断内部状态)。
    • PRNG 的缓解措施 (散列种子、重新播种、保护输出)。
  18. 特定 PRNG 的原理和漏洞 (LCG, LFSR)。
  19. 如何使用 PRNG 构建流密码 ($E_k(m) = m \oplus \text{PRNG}(k)$)。
  20. 流密码的优点和安全性依赖 (取决于 PRNG 安全性、种子必须只使用一次、周期长度)。
  21. 流密码的局限性 (只确保保密性，消息仍可被修改)。

示例考题

  1. 简述对称密码的工作原理，并列出至少三种对称密码提供的安全服务。请解释为什么在没有秘密密钥的情况下，解密密文是计算上困难的。
    • 参考答案：对称密码使用相同的秘密密钥进行加密和解密。Alice 用共享密钥 $k$ 和加密算法 $E_k$ 将明文 $m$ 加密成密文 $c=E_k(m)$。Bob 收到 $c$ 后，用相同的密钥 $k$ 和解密算法 $D_k$ 将其解密回明文 $m=D_k(c)$。提供的安全服务包括保密性 (Confidentiality)、完整性 (Integrity)、认证 (Authentication)、不可否认性 (Non-Repudiation)。在没有秘密密钥 $k$ 的情况下，密码系统被设计为计算上困难 (computationally hard) 从密文 $c$ 中恢复明文 $m$ 或密钥 $k$。这是因为密钥空间非常大 (例如 128 比特密钥对应 $2^{128}$ 种可能)，暴力破解不可行。
  2. 请定义唯密文攻击 (COA) 和已知明文攻击 (KPA)。解释选择明文攻击 (CPA) 如何比 KPA 更强，并举例说明 CPA 的应用场景。
    • 参考答案：唯密文攻击 (COA) 中，攻击者只能访问一个或多个由同一密钥加密的密文，目标是恢复部分或全部明文、密钥或解密算法。已知明文攻击 (KPA) 中，攻击者除了密文外，还拥有一些由同一密钥加密的明文/密文对，目标是恢复密钥或解密算法。选择明文攻击 (CPA) 中，攻击者可以选择任意明文并获得对应的密文，这使得 CPA 比 KPA 更强，因为攻击者可以精心构造明文来探测密码系统的特定弱点。即使对 KPA 有抵抗力的密码也可能对 CPA 脆弱。CPA 的一个应用场景是，攻击者向敌方系统输入特定的情报，希望这些情报被加密并发送回来，从而截获对应的密文，形成选择明文/密文对来分析密钥。
  3. 解释什么是维吉尼亚密码 (Vigenere Cipher)，以及如何使用重合指数 (Index of Coincidence) 来确定维吉尼亚密码的密钥长度。
    • 参考答案：维吉尼亚密码是一种多表替换密码，它使用一个重复的单词作为秘密密钥，加密过程是将明文与重复密钥进行模 26 加法。重合指数 (IC) 是一种统计度量，用于评估文本中随机选取两个字母相同的概率。已知标准英语文本的 IC 约为 0.0667，而纯随机文本的 IC 约为 0.0385。破解维吉尼亚密码的关键步骤是确定密钥长度 $N$。这是通过将密文切片为 $N$ 个部分，每个切片包含密文中所有位置相隔 $N$ 的字母。然后，计算每个切片的重合指数并求平均值。对不同的 $N$ 值重复此过程。平均重合指数最接近英语标准值 (0.0667) 的那个 $N$ 很可能就是密钥的长度。这是因为每个切片在密钥的某个字母作用下，相当于一个单表替换密码，而单表替换不改变其内部的字母频率分布特性，因此其 IC 会接近英语的 IC。
  4. 讨论一次性密码本 (OTP) 完美安全 (Perfectly secure) 的条件是什么，并解释为什么实践中很少使用 OTP 进行通用通信。
    • 参考答案：一次性密码本 (OTP) 是完美安全 (perfectly secure) 的，前提是满足三个条件：1. 秘密密钥必须是真正随机的 (truly random)。2. 明文不能重复 (plaintext does not repeat) (更准确地说，密钥流不能重复)。3. 密钥流不能重复 (keystream does not repeat)。其完美安全的原理在于，将一个真正随机的密钥加到明文上，产生的密文也是真正随机的，从密文中无法获得关于明文的任何信息。实践中，OTP 很少用于通用通信，主要原因在于其核心问题：密钥必须与消息长度相同。这意味着要加密 1GB 的数据，需要预先共享 1GB 的秘密密钥。这带来了巨大的密钥分发 (key distribution)、密钥存储和密钥销毁 (key destruction) 问题，尤其对于大容量通信而言非常不切实际。它通常只用于超安全、低带宽通信场景。
  5. 什么是伪随机数生成器 (PRNG)？解释为什么在密码学中需要使用密码学安全伪随机数生成器 (CSPRNG)，以及 CSPRNG 的种子来源 (entropy) 对于其安全性的重要性。
    • 参考答案：伪随机数生成器 (PRNG) 是一种算法，它基于一个初始的“种子”数据生成一个看起来统计上随机的数字序列。由于计算机是确定性的，无法产生真正的随机性，因此需要 PRNG 来模拟随机性。密码学安全伪随机数生成器 (CSPRNG) 是一种特殊的 PRNG，其设计使得攻击者在不知道种子的情况下，无法从输出序列中预测未来的输出或推断出先前的输出，从而使其适用于密码学应用。CSPRNG 的安全性很大程度上依赖于其种子来源的随机性，即熵 (entropy)。如果种子不是真正随机的，或者熵不足，攻击者可能会通过猜测、暴力破解或分析种子的来源来重现或预测 PRNG 的输出序列。例如，如果种子来源于可预测的系统状态或用户输入，攻击者可能利用这些信息来破解 PRNG，进而危及整个密码系统的安全。因此，从外部的、真正随机的源收集高熵的种子对于 CSPRNG 的安全性至关重要。

希望这份笔记对您有所帮助！

更新于 2025-03-19 
CC BY-NC-SA 4.0
计算机和网络安全
返回 | 主页
0%