计算机和网络安全课程笔记 Week 5

Nite 收录于笔记和计算机和网络安全

2025-03-19 约 1800 字预计阅读 9 分钟

阅读 PDF

RSA 攻击 (Attacks on RSA)

基于中国剩余定理 (CRT) 的攻击

中国剩余定理 (Chinese Remainder Theorem, CRT) 可用于攻击 RSA 公钥 $(n, e)$。攻击者通过收集具有相同加密指数 $e$ 但不同模数 $n$ 的密文消息。

如果 Alice 使用相同的消息 $m$ 向三个接收者发送密文，他们的公钥分别为 $(n_1, e), (n_2, e), (n_3, e)$，Eve 可以使用 CRT 求解以下联立方程组来找到 $m^e$：

$$ C_1 \equiv m^e \pmod{n_1} \ C_2 \equiv m^e \pmod{n_2} \ C_3 \equiv m^e \pmod{n_3} $$

其中 $\gcd(n_i, n_j) = 1$ (即 $n_i$ 和 $n_j$ 互质)。由于 $e$ 是已知的，可以使用对数运算从 $m^e$ 中恢复 $m$。

小加密指数攻击 (Small Encryption Exponent Attack)

也称为 Coppersmith 攻击 (Coppersmith’s attack)，这种攻击利用了加密指数选择不当，导致 $m^e < n$ 的情况。

如果 $m^e < n$，那么 $C = m^e \pmod n = m^e$。在这种情况下，可以通过计算 $C$ 的整数 $e$ 次方根来直接计算出消息 $m$。选择小的加密指数通常是为了提高 RSA 加密的速度。

使用小加密指数时，不应该将相同消息（或略有变化的消息）发送给多个实体。通过对明文加盐 (salting the plaintext)，即填充随机比特，可以帮助避免这种攻击。

小解密指数攻击 (Small Decryption Exponent Attack)

小解密指数常见于小型设备，因为小的 $d$ 可以提高解密效率。然而，应该避免使用小的解密指数。

存在算法可以从 $(n, e)$ 计算出 $d$，如果 $d$ 的比特数小于模数 $n$ 比特数的约四分之一。

前向搜索攻击 (Forward Search Attack)

由于加密密钥是公开的，如果消息空间 (message space) 很小或可预测，攻击者可以通过对消息空间进行暴力破解来尝试猜测消息。

通过对明文加盐 (salting the plaintext)，添加随机数，可以帮助防止这种攻击。

例如，在一个股票交易系统中，消息格式可能为 “{BUY, SELL} {DDDD} {TICKER}”。如果只有 1000 个 Ticker，可能的消息总数 $|M|$ = 2 (BUY/SELL) $\times$ 10000 (DDDD) $\times$ 1000 (TICKER) = 20,000,000。以每秒 100 万次猜测的速度，只需 20 秒就可以猜测到传输的消息。

基于同态性质的攻击 (Attacks based on Homomorphic Properties)

RSA 加密是同态的 (homomorphic)。假设 $c_1 = m_1^e \pmod n$ 且 $c_2 = m_2^e \pmod n$，那么 $c_1 \times c_2 = (m_1 \times m_2)^e \pmod n$。

利用这一性质，可以使用自适应选择密文攻击 (adaptive chosen ciphertext attack) 攻击 RSA。

攻击场景：Eve 想让 Alice 解密一个原定发送给 Bob 的密文 $c = m^e \pmod n$。Eve 向 Alice 发送一个经过改造的密文 $c’ = c \cdot r^e \pmod n$，其中 $r \in Z_n^\times$ 是一个随机选择的“致盲因子” (blinding factor)。

Alice 计算 $(c’)^d = (c \cdot r^e)^d \pmod n = c^d \cdot (r^e)^d \pmod n = m \cdot r \pmod n$。如果 Alice 将此结果透露给 Eve，Eve 可以通过计算 $(m \cdot r) \cdot r^{-1} \pmod n = m \pmod n$ 来“解除致盲” (unblind) 并恢复原始消息 $m$。

数字签名 (Digital Signatures)

签名用于将作者与其文档绑定。

签名所需属性 (Desirable Properties for a Signature)

可认证的 (Authentic): 足够相信签名者是故意签署了文档。
不可伪造的 (Unforgeable): 证明只有签名者才能签署该文档，其他人不能。
不可重用的 (Non-reusable): 签名本质上与文档绑定，不能转移到其他文档。
不可篡改的 (Unalterable): 签名后不能被更改。
不可否认性 (Non-repudiation): 签名者事后不能否认他们签署了文档（重要）。

这些属性可能受到攻击，设计使用签名的系统时必须考虑这些攻击。

数字签名基本原理 (Basic Digital Signature Principle)

我们有：$m$ - 要签名的消息，$k$ - 秘密密钥，$F$ - 签名方案（函数），$S$ - 签名。

$S = F(m, k)$

消息 $m$ 使用只有签名者知道的秘密密钥 $k$ 进行签名，通过签名方案 $F$ 将签名 $S$ 绑定到消息 $m$。给定 $(m, S)$，任何人无需秘密密钥 $k$ 即可验证签名。不可否认性通过 $k$ 的保密性实现。

基于公钥的数字签名 (Digital Signatures with Public Keys)

假设 Alice 希望签署消息并发送给 Bob。

密钥生成:

Alice 生成两个密钥：验证密钥 (verifying key) $A_v$（公钥）和签名密钥 (signing key) $A_s$（私钥）。
$A_v$ 发布在公钥目录 (public directory) 中。
$A_s$ 保密。

签名生成:

Alice 选择 $n$ 个随机比特 (random bits)：$r = {0, 1}^n$。
Alice 对消息进行哈希 (hash)，得到消息摘要 (message digest)：$d = h(m)$。
Alice 生成签名：$S = \text{signature}(d, r, A_s)$。
Alice 将 $(m, S)$ 发送给 Bob。

签名验证:

Bob 从公钥目录获取 $A_v$。
Bob 计算 $d = h(m)$。
Bob 运行 $\text{verify}(d, A_v, S)$。

防止签名重放 (Preventing Signature Replay)

为什么在签名中包含 $r = {0, 1}^n$？

考虑以下场景：Alice 给 Bob 发送一张 100 美元的数字支票。Bob 将支票交给银行。银行验证签名有效并给 Bob 的账户存入 100 美元。有什么可以阻止 Bob 再次兑现同一张支票？(即执行重放攻击 (replay attack))。

随机值 $r$ 称为 Nonce (或随机数)，用于避免重放。银行会记录所有从 Alice 那里见过的 Nonce。

签名攻击模型 (Signature Attack Models)

通用伪造 (Universal Forgery): 攻击者可以从公钥 $A_v$ 和消息/签名对 $(m, S)$ 中恢复私钥 $A_s$。
选择性伪造 (Selective Forgery): 攻击者可以针对选定的消息或消息类别伪造签名。
存在性伪造 (Existential Forgery): 攻击者可以针对已知消息伪造签名。这在理论上是可能的（基于目前可用的资源）。

基于 RSA 的朴素签名协议 (Naïve Protocol based on RSA)

一个基于 RSA 的朴素协议可能如下。

密钥生成:

$n = pq$，其中 $p, q$ 是大素数。
$d \times e \equiv 1 \pmod{\phi(n)}$，$e$ 与 $\phi(n)$ 互质。
$A_v = (n, e)$ 作为公钥/验证密钥。
$A_s = (n, d)$ 作为私钥/签名密钥。

签名生成:

假设 $m \in Z_n^\times$。
$S = m^d \pmod n$ — 使用 RSA 解密指数进行签名。

签名验证:

$S^e = (m^d)^e \pmod n = m \pmod n$ — 使用 RSA 加密指数进行验证。

朴素协议的问题 (Problem with Naïve protocol)

Eve 可以欺骗 Alice 签署某个消息 $m$。基于 RSA 的同态性质：

如果 $s_1 = m_1^d \pmod n$ 且 $s_2 = m_2^d \pmod n$，那么 $s_1 s_2 = (m_1 m_2)^d \pmod n$。

攻击朴素 RSA 方案:

Eve 希望 Alice 签署一个隐藏的消息 $m$。
Eve 随机选择 $r \in Z_n^\times$。
Eve 计算 $m’ = m \times r^e \pmod n$。
Eve 要求 Alice 签署 $m’$。
Alice 返回 $s’ = (m’)^d \pmod n = (m \times r^e)^d \pmod n = m^d \times r^{ed} \pmod n = m^d \times r \pmod n$。
Eve 计算 $s = s’ \cdot r^{-1} \pmod n = (m^d \cdot r) \cdot r^{-1} \pmod n = m^d \pmod n$。

对 $(m, s)$ 而言，$s = m^d \pmod n$，所以 $(m, s)$ 是一个有效的消息-签名对。Eve 成功欺骗 Alice 签署了隐藏消息 $m$。

PKCS#1 签名方案 (PKCS#1 Signature Scheme) (RFC2313)

PKCS#1 签名方案处理的是消息的哈希而不是原始消息，这快得多。

签名生成:

$n = pq$ (1024 位模数)。
Alice 计算 $D = h(m)$ (160 位哈希)。
定义加密块 (encryption block): EB = [ 00 | BT | PS | 00 | $D$ ]
- PS: 填充 (Padding)，使块长度与模数相同。
- BT: 块类型 (Block type)，决定填充样式。
- EB 长度为 864 位 + 160 位 = 1024 位。
Alice 计算 $S = \text{EB}^d \pmod n$。
Alice 发送 $(S, m)$。

签名验证:

$S = \text{EB}^d \pmod n$。
Bob 计算 $S^e \pmod n = \text{EB} \pmod n$。
Bob 检查前 864 位是否有效。
Bob 检查后 160 位是否有效 (即等于 $h(m)$)。

数字签名算法 (Digital Signature Algorithm, DSA)

数字签名算法 (DSA) 于 1991 年被 NIST 选为数字签名标准 (DSS)。

参数选择:

选择一个哈希函数 (Hash function) $H$。最初是 SHA-1，现在推荐 SHA-2。
选择密钥长度 $N$ 和 $L$，使得 $N < L$。
选择一个 $N$ 比特的素数 $q$。
选择一个 $L$ 比特的素数模数 (prime modulus) $p$，使得 $p-1$ 是 $q$ 的倍数。
选择一个随机整数 (random integer) $h$，使得 $1 < h < p-1$。
计算 $g = h^{(p-1)/q} \pmod p$。如果 $g=1$，则用不同的 $h$ 重复。

密钥生成与分发:

秘密密钥 (Secret key) $c$ 在 $0 < c < q$ 中随机选择。
计算公钥 (Public key): $y = g^c \pmod p$。
同时提供 $p, q, g$ 参数作为公钥的一部分。

签名生成:

选择随机数 $k \in Z_q^\times$，其中 $1 < k < q$。
- 必须为每条消息唯一。
计算 $r = (g^k \pmod p) \pmod q$。
- 如果 $r = 0$，则用不同的 $k$ 重复。
计算 $s = k^{-1} (H(m) + c \cdot r) \pmod q$。
- 如果 $s = 0$，则用不同的 $k$ 重复。
签名为：$(r, s)$。

签名验证:

验证 $0 < r < q$ 且 $0 < s < q$。
计算 $w = s^{-1} \pmod q$。
计算 $u_1 = (H(m) \times w) \pmod q$。
计算 $u_2 = (r \times w) \pmod q$。
计算 $v = (g^{u_1} \times y^{u_2} \pmod p) \pmod q$。
如果 $v == r$，则签名有效。

DSA 的正确性基于其数学原理。

DSA/DSS 注意事项:

DSA 的安全性基于随机签名值 $k$ 的属性。
重复使用相同的 $k$，使用可预测的 $k$，或者在多次签名中泄露 $k$ 的少量比特，都足以泄露秘密密钥 $c$。
使用同步求幂 (simultaneous exponentiation) 可以将 DSA 签名验证速度提高一倍。
基于 RSA 的签名易受量子计算 (quantum computing) 威胁。使用单向哈希函数 (one-way hash functions) 的替代数字签名（如 Lamport 签名 (Lamport signature)）可能更具抗量子性。
当前标准禁止生成新的 DSA 签名。但是，验证使用 DSA 生成的签名仍然被接受。

认证 (Authentication)

核心问题 (Core Problem)

Bob 如何知道与他通信的 Alice 不是 Eve？

认证的目的 (Purpose of Authentication)

认证是一种建立身份的方法。Bob 需要确保通道另一端的实体是 Alice。

确保 Alice 的身份。
确保 Alice 积极参与了交互。

目标：在不安全信道 (insecure channel) 上，存在活跃攻击者 (active attacker)，且没有共享秘密 (no shared secrets) 的情况下实现这一目标。

注意：认证必须与密钥交换 (key exchange) 结合使用，以避免在认证后发生会话劫持 (session hijacking)。

身份认证协议目标 (Objectives of Identification Protocols)

如果 Alice 和 Bob 都是诚实的，Alice 应该能够成功认证自己，即 Bob 在协议完成后会验证 Alice 的身份。
Bob 不应该能够重用与 Alice 的认证会话来冒充她在与其他方通信。
Eve 成功冒充 Alice 的概率应该是可以忽略的（计算上困难）。
即使在以下情况下，上述目标也应保持真实:
- Eve 见过许多 Alice 和 Bob 之间的认证会话。
- Eve 曾与 Alice 和/或 Bob 进行过认证。
- 多个认证会话同时运行。

认证的基础 (Basis of Identification)

你知道什么 (Something you know): 密码 (Password)，PIN 码 (PIN)，秘密密钥 (secret key)，母亲的娘家姓，宠物的颜色等。
你拥有什么 (Something you have): 磁卡，智能卡，物理密钥，数字安全密钥，带有 Google Authenticator 的手机等。
你是谁 (Something you are): 生物识别 (Biometrics): DNA，签名，指纹，声音，视网膜模式，手形，打字习惯/分析等。
- 生物识别在实际情况中存在问题:
  - DNA 和指纹会留在任何地方。
  - 如果你眼睛青了或手指受伤了怎么认证？

认证的例子 (Examples of Authentication)

作为通信前验证身份的前奏:
- 在更新“amazon.com”上的卡详情前确认电子邮件的发送者。
促进对资源的访问:
- 本地/远程访问计算资源（密码，OTP）。
- 从 ATM 取款（银行卡和 PIN 码）。
- 允许通过 Web 服务器代理通信。
- 允许物理访问限制区域（刷卡）。
- 边境检查（护照，指纹）。
促进资源跟踪和计费:
- 手机接入。

认证攻击 (Authentication Attacks)

冒充攻击 (Impersonation): 攻击者伪装成合法用户。
中继攻击 (Relay): 攻击者拦截并在另一个连接中重放消息。
交错攻击 (Interleaving): 冒充攻击的一种，涉及选择性地组合来自一个或多个先前或并发会话的信息。
反射攻击 (Reflection): 一种交错攻击，涉及将正在进行的认证会话中的信息发送回发起者。
强制延迟攻击 (Forced Delay): 攻击者拦截消息并在稍后某个时间点中继（与重放不同！）。
选择文本攻击 (Chosen Text): 一种挑战-应答攻击，攻击者选择挑战，试图提取秘密密钥。

密码 (Passwords)

密码是一种简单（且弱）的认证方法。

Alice 创建一个秘密密码 (secret password)，只与 Bob 在某个时间点共享。
要认证时，Alice 透露她的姓名和密码。

密码通常在服务器上哈希存储 (stored hashed)，以提高安全性。如果服务器被入侵，这些哈希需要被破解才能揭示密码。

密码问题 (Problems with Passwords)

密码可能被窃听 (eavesdropped) 和重放 (replayed)。通过使用 Diffie-Hellman 和对称密码 (symmetric crypto) 保护通道可以部分解决。但仍然容易受到击键记录器 (keyloggers)、设备盗窃等攻击。
密码通常来自小密钥空间 (small keyspace)，或因难以记忆而被重复使用。许多网站仍然限制密码长度。
字典攻击 (Dictionary attacks) 非常可行。
- 由于密码难以生成和记忆，大多数人工生成的密码可以在字典中找到。
- 预先计算字典中所有密码的哈希。
- 收到密码哈希后，在预计算表中查找。如果存在，密码即已知。
- 使用大型密码表的字典攻击易于重用和共享。
- 攻击的重大扩展：彩虹表 (Rainbow tables) 使用非常紧凑的存储。
一个网站被入侵可能导致使用相同密码的所有网站被入侵。
人们在设置机器难以破解的密码方面表现不佳。

密码加盐 (Salting Passwords)

对于密码 $p$ 和哈希函数 $h$，不使用 $h(p)$ 作为密码哈希，而是生成一个随机字符串 $s$，使用 $h(p \parallel s)$。字符串 $s$ 称为盐 (salt)。

盐通常与密码哈希存储在一起。盐是随机选择的。这可以阻止依赖大规模预计算的字典攻击。然而，如果盐已知，仍然可以进行暴力字典攻击。

旧版 UNIX 密码使用 DES 作为哈希函数，并使用 2 字节的公开盐 (Public Salt) 来修改扩展函数，防止使用标准 DES 芯片进行破解。哈希在 /etc/passwd 文件中对所有用户可见（不好！）。如今，哈希密码和盐被锁定在单独的文件中，不可读。

暴力破解哈希 (Brute Force Hashes)

在 CPU 上每秒可以破解数百万个密码，在 GPU 上每秒可以破解数十亿个密码。

对于由 [a-zA-Z0-9] 和符号组成的 8 个字符密码，使用 SHA256 哈希，Antminer S9 平均需要 1 天破解。10 个字符则需要 25 天。

暴力破解密码哈希很容易并行化：N 台机器可以提供 N 倍加速。

标准哈希算法 (MD5, SHA1, SHA256) 不适合用于密码哈希。哈希算法设计目的是快速运行。密码哈希理想情况下应该慢，以减缓暴力破解攻击。即使有盐，暴力破解这些算法也是微不足道的。

现代密码哈希 (Modern password hashing)

bcrypt：一个用于密码的密钥派生函数 (key derivation function)，强烈建议用于所有网站。它提供了密钥拉伸 (key stretching) 功能，执行 $2^c$ 次哈希迭代，其中 $c$ 是一个可调的成本参数。随着时间的推移，可以增加 $c$ 使其变慢。
scrypt：bcrypt 旨在通过增加时间使哈希更昂贵，但仍容易受到硬件攻击。scrypt 旨在通过使用更多空间使密码哈希更困难。它通过使用大量内存来使硬件实现变得困难。其核心算法在 Litecoin 中使用，以阻止基于硬件的挖矿实现。

一次性密码 (One Time Passwords, OTP)

在一次性密码方案中，每个密码只使用一次，例如为了阻止窃听者和重放攻击。

有多种变体:

共享的一次性密码列表。
挑战/应答表 (Challenge/response table)。
顺序更新一次性密码（例如，用户在使用 $k_i$ 时创建并上传 $k_{i+1}$）。
基于单向函数 (one-way function) 的一次性序列（例如，Lamport 一次性密码方案）。

Lamport 一次性密码 (Lamport’s One Time Passwords)

设置 (setup)（最多可使用 $n$ 次）:

Alice 选择一个随机密钥 $k$，并计算哈希链 (hash chain) $w = h^n(k)$，其中 $h^n(k) = h(h^{n-1}(k))$。
Alice 将 $w$ 发送给服务器，并将计数器 $c$ 设置为 $n-1$。

认证 (Authentication):

Alice 将 $c = h^c(k)$ 发送给服务器，并递减计数器 $c$。
服务器验证 $h(c) = w$，并将 $w$ 重置为 $c$。

优点:

服务器上不存储任何秘密。
防止来自窃听的重放攻击。

缺点:

在需要设置新哈希链之前，认证次数有限。
如果原始秘密被泄露，容易受到预演攻击 (pre-play attack)。

HOTP (HMAC-Based One-Time Password Algorithm)

HOTP 定义在 RFC 4226 中。

设置:

客户端和服务器约定一个大的（$\ge$ 160 比特）秘密密钥 $k$。
客户端和服务器同步一个 8 字节的计数器 (counter) $c$，该计数器随时间增加。

认证:

定义 HOTP$(k, c) = \text{HMAC-SHA-1}(k, c) \pmod{10^d}$。
客户端计算 $w = \text{HOTP}(k, c)$ 并发送给服务器。
服务器验证 $w$ 是否为当前 $c$ 值的 HOTP$(k, c)$。
- $\pmod{10^d}$ 只返回 HMAC 结果的最低 $d$ 位十进制数字。
- 认证通常允许一个小的 $c$ 值“容错窗口” (window of error)，以应对用户输入慢或时钟不同步。

TOTP (Time-Based One-Time Password Algorithm)

TOTP 定义在 RFC 6238 中，是 HOTP 的扩展。它指定 HOTP 中的计数器 $c$ 应为:

$c = \lfloor (\text{Current time} - T_0) / X \rfloor$

其中 $T_0$ 和 $X$ 是预先约定的秒数。例如，$X = 30$ 秒将使密码每 30 秒更改一次。$T_0$ 可能是用户注册时间或 Unix 时间零点。

挑战-应答认证 (Challenge-Response Authentication)

一个实体通过展示其对秘密的了解来向另一个实体证明其身份，而无需透露秘密本身。这通过对一个时变挑战 (time-variant challenge) 提供应答 (response) 来完成。应答依赖于挑战和秘密。

时变参数对于应对重放攻击和交错攻击至关重要，以提供唯一性和及时性保证，并防止某些选择密文攻击。时变参数的例子包括 Nonce、序列号 (Sequence Numbers) 和时间戳 (Timestamps)。

使用对称密码的挑战-应答认证 (Challenge-Response using Symmetric Crypto)

Bob 和 Alice 拥有一个共享秘密 $k$，并约定使用某个带密钥的加密或哈希算法 $E_k$。

Alice 发起与 Bob 的通信。
Bob 生成一个 Nonce $r$，并发送给 Alice。
Alice 生成一个 Nonce $r_c$，并将 $r_c$ 和 $E_k(r \parallel r_c)$ 发送给 Bob。
Bob 计算 $E_k(r \parallel r_c)$，并与 Alice 发送的进行比较。

使用非对称密码的挑战-应答认证 (Challenge-Response using Asymmetric Crypto)

Alice 将其公钥 $A$ 发布给所有人，Bob 持有副本（并在之前的某个时间点验证了其真实性）。

Alice 发起与 Bob 的通信。
Bob 生成一个 Nonce $r$，并发送给 Alice。
Alice 签名 (sign) Nonce，即 $\text{sign}_A(r)$，并将结果发送给 Bob。
Bob 使用 Alice 的公钥验证 (verify) 签名。

无需存储共享秘密。

零知识证明 (Zero Knowledge Proofs, ZKP)

零知识证明 (ZKP) 的设计目的是让证明者 (prover) 证明其对秘密的了解，而不透露任何关于秘密的信息。ZKP 通常包含许多挑战-应答回合 (challenge-response rounds)。

攻击者在单次回合中可以以很小的概率欺骗 (cheat) 成功。在一个好的 ZKP 协议中，欺骗成功的概率随着交互回合数的增加呈指数下降。对于足够多的回合，成功欺骗者的概率实际上为 0。零知识证明协议通常很难设计出来，但在挑战-应答认证中有应用。

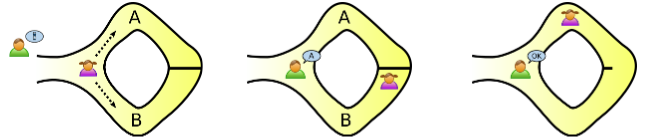
阿里巴巴洞穴示例 (Ali Baba’s Cave Example)

这是 Quisquater & Guillou (1989) 的一个著名例子。

阿里巴巴的洞穴有一个活板门/暗门 (trapdoor)，只有知道秘密密码 (secret password) 才能打开。Peggy (证明者) 声称知道密码，并想说服 Victor (验证者) 她知道，但不想告诉 Victor 密码。

Victor 站在入口处，Peggy 进入任意一条分支 (A 或 B)。
Peggy 站在活板门旁边，Victor 进入洞穴，并喊叫让 Peggy 从 A 或 B 出来。

如果 Peggy 知道密码，她总是能做到 Victor 要求的。如果她不知道，成功 $n$ 次的概率是 $2^{-n}$。

Peggy 不能欺骗 Victor。Peggy 第一次失败，Victor 就知道 Peggy 不合法。因此，每个回合被称为一个认证回合 (accreditation)。通过每个认证回合，确定性越来越好，直到达到所需的水平。

ZKP 的属性:

Victor 无法从协议中学习到任何信息，除了 Peggy 知道某个秘密。
Peggy 不能欺骗 Victor。
Victor 不能冒充 Peggy 去欺骗第三方。
参考：就餐密码学家问题 (Dining cryptographers problem)。

潜在考点与示例考题

RSA

考点: RSA 的密钥生成、加解密过程；基于同态性质的自适应选择密文攻击的原理和过程；小加密指数攻击的条件和恢复消息的方法；防止小加密指数攻击和前向搜索攻击的方法（加盐）；小解密指数的风险。

示例考题:

描述 RSA 密钥生成、加密和解密的基本步骤。
- 参考答案: 参见 RSA 算法部分。
解释 RSA 的同态性质是什么？攻击者如何利用 RSA 的同态性质进行自适应选择密文攻击？请描述攻击过程。
- 参考答案: 参见 RSA 算法 -> 基于同态性质的攻击部分。
什么是 RSA 的小加密指数攻击？这种攻击成立的条件是什么？攻击者如何在这种条件下恢复原始消息？如何缓解这种攻击？
- 参考答案: 参见 RSA 攻击 -> 小加密指数攻击部分。
除了小加密指数攻击，RSA 还可能受到哪些攻击？如何防御其中的前向搜索攻击？
- 参考答案: 参见 RSA 攻击 -> 小解密指数攻击, 前向搜索攻击部分，防御前向搜索攻击主要依靠加盐。

数字签名

考点: 数字签名的重要属性（特别是不可否认性）；基于公钥的数字签名流程（生成与验证）；为什么在签名中包含随机 Nonce (防止重放攻击)；签名攻击模型（通用、选择性、存在性伪造）；基于 RSA 的朴素签名方案的漏洞（利用同态性质进行伪造）及其攻击过程；PKCS#1 签名方案与朴素方案的区别和优势（处理哈希）；DSA 的基本参数、密钥生成、签名生成和验证过程；DSA 的安全性依赖（随机签名值 k）以及泄露 k 的风险；DSA 的当前使用状态。

示例考题:

数字签名应具备哪些重要的属性？请解释不可否认性的意义。
- 参考答案: 参见数字签名 -> 签名所需属性部分。
基于公钥的数字签名方案中，签名生成和验证的基本流程是怎样的？为什么在签名生成时通常会包含一个随机数 (Nonce)？
- 参考答案: 参见数字签名 -> 基于公钥的数字签名, 防止签名重放部分。
描述基于 RSA 的朴素签名方案的签名生成和验证过程。解释该朴素方案存在什么安全漏洞？攻击者如何利用 RSA 的同态性质来伪造签名？
- 参考答案: 参见数字签名 -> 基于 RSA 的朴素签名协议, 朴素协议的问题部分。
DSA 是一种数字签名算法。请概述其签名生成和验证过程。DSA 的安全性主要依赖于什么？如果用于签名生成的随机数 $k$ 被泄露或可预测，会带来什么安全风险？
- 参考答案: 参见数字签名 -> 数字签名算法 (DSA), DSA/DSS 注意事项部分。

认证

考点: 认证的核心问题和目标；认证的三个基础（你知道、你拥有、你是谁）的优缺点；常见的认证攻击类型（冒充、重放、反射、交错等）；密码认证的问题（字典攻击、重放、弱密码等）；防御字典攻击和提高密码安全性的方法（哈希存储、加盐、密钥派生函数 bcrypt/scrypt）；一次性密码 (OTP) 的原理和不同类型（Lamport, HOTP, TOTP）的特点；挑战-应答认证的原理（利用时变参数）以及基于对称/非对称密码的实现方式；零知识证明 (ZKP) 的基本概念和属性（证明知识不泄露信息、不可欺骗、不可冒充）。

示例考题:

认证的核心问题是什么？在不安全信道上，在没有共享秘密的情况下，认证的目标是什么？认证应与什么技术结合使用以避免会话劫持？
- 参考答案: 参见认证 -> 核心问题, 认证的目的部分。
认证的三个基础是什么？请分别举例并简述其特点或潜在问题。
- 参考答案: 参见认证 -> 认证的基础部分。
列举至少三种常见的认证攻击类型，并简要解释其原理。
- 参考答案: 参见认证 -> 认证攻击部分。
基于密码的认证存在哪些主要问题？什么是字典攻击？如何利用加盐来防御字典攻击？请比较 bcrypt 和 scrypt 这两种现代密码哈希方法的不同侧重点。
- 参考答案: 参见认证 -> 密码问题, 密码加盐, 现代密码哈希部分。
解释一次性密码 (OTP) 的基本原理。请简述 HOTP 和 TOTP 这两种一次性密码算法的主要区别。
- 参考答案: 参见认证 -> 一次性密码, HOTP, TOTP 部分。
什么是挑战-应答认证？其核心思想是什么？为什么需要使用时变参数？简述基于非对称密码的挑战-应答认证流程。
- 参考答案: 参见认证 -> 挑战-应答认证部分。
解释零知识证明 (ZKP) 的基本概念。ZKP 的三个重要属性是什么？请简述阿里巴巴洞穴示例如何体现零知识证明的思想。
- 参考答案: 参见认证 -> 零知识证明部分。