计算机和网络安全课程笔记 Week 4
目录
密钥交换
基础概念
- 密钥建立 (Key Establishment):指两个或多个参与方为了后续密码学用途而共享密钥的过程。
- 密钥管理 (Key Management):支持密钥建立和维护参与方之间持续密钥关系(包括更新密钥)的一系列过程和机制。这包括密钥协商 (Key agreement) 和密钥传输 (Key transport)。
- 在一个拥有 $n$ 个参与方的对称密钥网络中,若任意两个参与方都需要安全通信,则总共需要 $n(n-1)/2$ 把共享密钥。这通常表示为 $n^2$ 数量级。例如,对于 Alice, Bob, Carol 和 Dave 四个参与方,需要 $4 \times 3 / 2 = 6$ 把密钥。
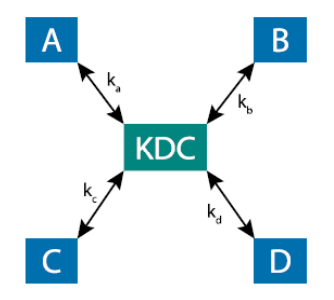
简单密钥分发中心 (Naïve Key Distribution Centre, KDC)
简单 KDC 是通过一个受信任的第三方(KDC)来帮助参与方建立共享密钥的方法。
-
协议 (Protocol):
- Alice → KDC: 我想和 Bob 通话。
- KDC → Alice:
- KDC 选择一个随机的会话密钥 $k_{ab}$。
- 返回加密消息:$E_{k_a}(k_{ab})$ 和 $E_{k_b}(k_{ab}, \text{“for talking to Alice”})$。($k_a$ 是 Alice 和 KDC 之间的密钥,$k_b$ 是 Bob 和 KDC 之间的密钥)。
- Alice 解密 $E_{k_a}(k_{ab})$ 得到会话密钥 $k_{ab}$。
- Alice → Bob: 发送 $E_{k_b}(k_{ab}, \text{“for talking to Alice”})$。
- Bob 使用密钥 $k_b$ 解密消息,得到会话密钥 $k_{ab}$。
- Alice 和 Bob 现在共享密钥 $k_{ab}$。
-
问题 (Problems):
- 密钥分发中心 (KDC) 是一个单点故障 (single point of failure),容易受到攻击。
- 缺乏认证 (No authentication)。
- 可伸缩性差 (Poor scalability)。
- 速度慢 (Slow)。
Merkle 谜题 (Merkle’s Puzzles)
Merkle 谜题是一种无需第三方即可在 Alice 和 Bob 之间进行密钥交换的方法。
-
协议 (Protocol):
- Alice 创建 $N$ 个谜题 $P_1, P_2, \dots, P_N$,每个谜题形式为 $P_i = E_{p_i}(\text{“This is puzzle #}X_i\text{”, } k_i)$。
- $N \approx 2^{20}$。
- $p_i$ 是弱密钥,大小约 20 位。
- $k_i$ 是强密钥,大小约 128 位。
- $X_i, p_i, k_i$ 对于每个 $i$ 都是随机且不同的。
- Alice 将所有谜题 $P_1, P_2, \dots, P_N$ 发送给 Bob。
- Bob 随机选择一个谜题 $P_j$(其中 $j \in {1, 2, \dots, N}$)。
- Bob 通过暴力破解 (brute force / key space search) 找到密钥 $p_j$。
- Bob 解密谜题,恢复密钥 $k_j$ 和标识符 $X_j$。
- Bob 将 $X_j$ 未加密地发送给 Alice。
- Alice 通过查找 $X_j$ 的索引来找到 Bob 选择的密钥 $k_j$。
- Alice 和 Bob 现在共享密钥 $k_j$。
- Alice 创建 $N$ 个谜题 $P_1, P_2, \dots, P_N$,每个谜题形式为 $P_i = E_{p_i}(\text{“This is puzzle #}X_i\text{”, } k_i)$。
-
攻击 (Attacking Merkle’s Puzzles):
- 攻击者 Eve 需要平均破解一半的谜题才能找到包含 $X_j$ 的谜题(并因此获得 $k_j$)。
- 如果有 $2^{20}$ 个谜题,每个谜题都用 20 位弱密钥 $p_i$ 加密,Eve 平均必须搜索一半的密钥空间和一半的谜题。计算复杂度约为 $2^{19} \times 2^{19} = 2^{38}$。
- 如果 Alice 和 Bob 每秒可以尝试 10,000 个密钥,他们各自的步骤(Alice 生成,Bob 破解 $p_j$)大约需要 1 分钟 ($2^{19}$ 密钥)。加上通过无线链路传输所有谜题的时间,大约需要额外 1 分钟。
- 拥有类似资源的 Eve 攻击该系统大约需要一年时间。
- 注意:Merkle 谜题需要大量的带宽,不实用。
数论基础 (Number Theory Basics)
数论是许多公钥密码学的基础。
模 $n$ 整数 (Integers modulo $n$)
- 给定整数 $n \in \mathbb{Z}$,进行模 $n$ 的算术运算(只保留除以 $n$ 的余数)。
- 例如:$6 + 6 \equiv 12 \equiv 0 \pmod{12}$
- $5 - 9 \equiv -4 \equiv 8 \pmod{12}$
- $5 \times 11 \equiv 55 \equiv 7 \pmod{12}$
- 这组数称为 $Z_n$。例子是 $Z_{12} = {0, 1, 2, \dots, 11}$。
- $Z_n = {0, 1, 2, \dots, n-1}$。
- 加法和减法在 $Z_n$ 中表现良好。
- 加法是循环的:$n \times (1 + 1 + \dots + 1) = 0$。
- 每个元素 $a \in Z_n$ 都有对应的负元 $-a \in Z_n$,满足 $a + (n-a) \equiv n \equiv 0 \pmod{n}$。
- 乘法通常表现不好。
- 在 $Z_{12}$ 中,$3 \neq 0$ 且 $4 \neq 0$,但 $3 \times 4 = 0$。这些称为零因子 (zero-divisors)。
- 零因子没有乘法逆元 (inverses),因此不能进行除法。
乘法群 $Z_n^$ (Multiplicative Group $Z_n^$)
- 乘法群 $Z_n^*$ 是 $Z_n$ 中所有与 $n$ 互素 (coprime) 的元素 $a$ 的集合,即 $\text{gcd}(a, n) = 1$。
- $Z_n^* = {a \in Z_n \mid \text{gcd}(a, n) = 1}$。
- 例如:$Z_{21}^* = {1, 2, 4, 5, 8, 10, 11, 13, 16, 17, 19, 20}$。这排除了 0 和与 21 共享因子的元素。
- 在 $Z_n^*$ 中不能进行加法和减法。
- 在 $Z_n^*$ 中,乘法和除法(求逆元)是可行的:每个元素都有乘法逆元。
$Z_n^$ 的大小:欧拉函数 $\phi(n)$ (Size of $Z_n^$: Euler’s phi function $\phi(n)$)
- $Z_n^*$ 的大小是 $\phi(n)$,称为欧拉函数或欧拉总计函数 (Euler’s totient function)。
- $\phi(n)$ 是小于 $n$ 且与 $n$ 互素的正整数的数量。
- 如果 $p$ 是素数 (prime),则 $\phi(p) = p - 1$。
- 如果 $n, m$ 互素,则 $\phi(nm) = \phi(n)\phi(m)$。
- 如果 $p, q$ 是不同的素数,则 $\phi(pq) = \phi(p)\phi(q) = (p-1)(q-1)$。
- $\phi(n)$ 的计算通常需要 $n$ 的质因数分解 (prime factorisation)。质因数分解对于大数而言非常困难,RSA 的安全性就依赖于此。
循环乘法与生成元 (Cyclic Multiplication and Generators)
- 在 $Z_n^$ 中,乘法是循环的,循环长度是群的大小 $|Z_n^| = \phi(n)$。
- 最重要的性质:对于任何 $x \in Z_n^*$,$x^{\phi(n)} \equiv 1 \pmod n$。
- 这意味着使用大于 $\phi(n)$ 的幂是“无用”的。
- 有些元素可能会更快地“回到 1”。
- 有时存在元素 $g \in Z_n^$,其幂次可以生成 $Z_n^$ 中的所有元素,即 ${g^0, g^1, g^2, \dots, g^{\phi(n)-1}} = Z_n^*$。这样的 $g$ 称为生成元 (generator)。
- 生成元生成的序列长度最大可达 $\phi(n)$。
- 如果 $n$ 是素数 $p$,则 $Z_p^*$ 总是存在生成元,且序列长度为 $\phi(p) = p-1$。
逆元 (Inverses)
- 在 $Z_n^*$ 中,每个元素 $a$ 都存在逆元 $a^{-1}$,使得 $a \cdot a^{-1} \equiv 1 \pmod n$。
- 因为 $a^{\phi(n)} \equiv 1 \pmod n$,所以 $a^{-1} \equiv a^{\phi(n)-1} \pmod n$。
- 对于 $Z_p^*$($p$ 是素数),$a^{-1} \equiv a^{\phi(p)-1} \equiv a^{p-1-1} \equiv a^{p-2} \pmod p$。这基于费马小定理 (Fermat’s Little Theorem)。
- 示例 (Example): 在 $Z_{21}^*$ 中求 11 的逆元。
- 计算 $\phi(21) = \phi(3 \times 7) = \phi(3)\phi(7) = (3-1)(7-1) = 2 \times 6 = 12$。
- 逆元为 $11^{\phi(21)-1} = 11^{12-1} = 11^{11} \pmod{21}$。计算 $11^{11} \equiv 2 \pmod{21}$。
- 检查:$2 \times 11 = 22 \equiv 1 \pmod{21}$。
- 所以在 $Z_{21}^*$ 中,$11^{-1} = 2$。
裴蜀等式与逆元计算 (Bézout’s Identity and Inverse Calculation)
- 裴蜀等式 (Bézout’s Identity) 是一个高效计算两个大数最大公约数 (GCD) 的方法。
- 对于 $a, n \in \mathbb{Z}$,存在 $\lambda, \mu \in \mathbb{Z}$ 使得 $\lambda a + \mu n = \text{gcd}(a, n)$。
- 如果 $\text{gcd}(a, n) = 1$,则 $1 \equiv \lambda a + \mu n \equiv \lambda a \pmod n + \mu n \pmod n \equiv \lambda a \pmod n$。这意味着 $\lambda$ 是 $a$ 的模 $n$ 的逆元。
- 欧几里得算法 (Euclidean algorithm)(辗转相除法)可以高效地计算 $\text{gcd}(x, y)$ 并找到满足裴蜀等式的系数 $s, t$,即 $sx + ty = \text{gcd}(x, y)$。
- 扩展欧几里得算法 (Extended Euclidean algorithm) 就是用来找这个系数 $s$ 的。
- 该算法的时间复杂度是 $O(\log x + \log y)$,对于大数(如 $\ge 2048$ 位)也很高效。
- 因此,求 $x \in Z_n^*$ 的逆元 $x^{-1}$ 的另一种方法是利用扩展欧几里得算法找到满足 $sx + tn = 1$ 的 $s$,那么 $s$ 就是 $x$ 的逆元。
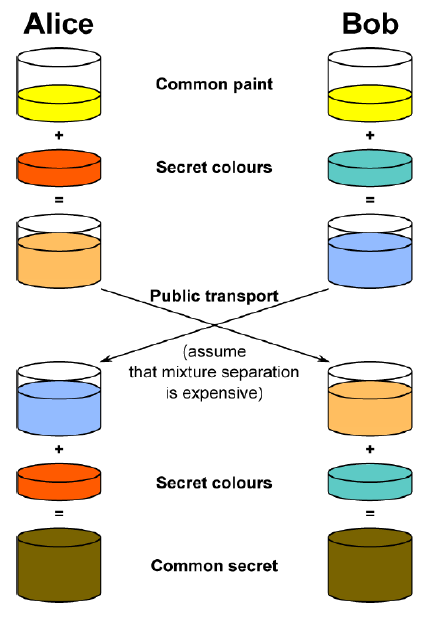
Diffie-Hellman 密钥交换 (Diffie-Hellman Key Exchange)
Diffie-Hellman 密钥交换 (Stanford, 1976) 是一种用于建立共享加密密钥的非对称 (asymmetric) 协议。它是 SSL, 智能卡等中的世界标准。
-
想法 (The rough idea):
- Alice 和 Bob 约定一个公共数 $g$。
- Alice 生成一个秘密随机数 $a$,并发送 $g^a$ 给 Bob。
- Bob 生成一个秘密随机数 $b$,并发送 $g^b$ 给 Alice。
- Alice 和 Bob 都可以计算出 $g^{ab}$,即他们的共享秘密。
- 窃听者 Eve 只能看到 $g, g^a, g^b$。假设取对数 (taking logarithms) 很困难,Eve 无法恢复 $a$ 或 $b$。
-
协议步骤 (Protocol Steps):
- Alice 和 Bob 约定一个大素数 $p$ 和 $Z_p^*$ 的生成元 $g$。
- Alice 选择一个随机数 $a$ ($1 < a < p$) 并发送 $g^a \pmod p$ 给 Bob。
- Bob 选择一个随机数 $b$ ($1 < b < p$) 并发送 $g^b \pmod p$ 给 Alice。
- Alice 计算 $(g^b)^a \pmod p = g^{ba} \pmod p$。
- Bob 计算 $(g^a)^b \pmod p = g^{ab} \pmod p$。
- 共享秘密是 $g^{ab} \pmod p$。
-
计算困难性 (Computing in $Z_p^*$ ):
- 在 $Z_p^*$ (p 为素数) 中容易的操作:生成随机数、乘法、幂运算 ($g^r \pmod p$)、求逆元、解线性方程组、解 $m$ 次多项式方程。
- 在 $Z_p^*$ 中困难的操作:离散对数问题 (Discrete Log Problem, DLP) 和 Diffie-Hellman 问题 (Diffie–Hellman Problem, DHP)。
-
Diffie-Hellman 的强度 (Strength of Diffie-Hellman Key Exchange):
- Diffie-Hellman 密钥交换的强度基于两个问题:
- 离散对数问题 (Discrete Logarithm Problem, DLP): 给定 $g$ 和 $g^a \pmod p$,很难计算出 $a$。
- Diffie-Hellman 问题 (Diffie-Hellman Problem, DHP): 给定 $g^a \pmod p$ 和 $g^b \pmod p$,很难计算出 $g^{ab} \pmod p$。
- 我们知道 DLP 难题蕴含 DHP 难题,但反之不一定成立 (DL ⇒ DH but it is not known that DH ⇒ DL)。
- 安全性基于数论技巧。
- 强度与对模数 $p$ 大小的数进行因数分解的难度成正比。
- 生成元 $g$ 可以比较小。
- 不要直接使用秘密 $g^{ab}$ 作为共享密钥,因为 $g^{ab}$ 的并非所有位都具有平坦分布 (flat distribution)。最好对其进行哈希处理 (hash it) 或用作伪随机数生成器 (PRNG) 的种子。
- 我们假设 DLP 和 DHP 在计算上是困难的,但没有形式化的证明。未来可能发现“容易”的解法。
- Diffie-Hellman 密钥交换的强度基于两个问题:
-
攻击 (Attacks on the Discrete Log Problem):
- 穷举搜索 (Exhaustive search):复杂度与 $p$ 的大小呈线性关系,因为 $Z_p^*$ 有 $p-1$ 个元素。如果 $p$ 有 $b$ 位,则 $p \approx 2^b$,复杂度约为 $O(2^b)$。
- 更高效的方法(复杂度 $O(2^{b/2})$):
- 小步大步算法 (Baby-step giant-step algorithm):一种时间-内存权衡的穷举搜索方法。
- Pollard’s rho 算法。
- Pohlig-Hellman 算法:对于特定结构的群有效。
- 对于大数 $p$,这些经典方法目前不实用。
- Shor’s Algorithm:存在一种高效的量子算法 (efficient quantum algorithm) 可以解决 DLP。
-
参数 $g$ 和 $p$ 的选择 (Selecting $g$ and $p$):
- 可以自行选择,但推荐使用 RFC 标准 (RFC 3526) 中定义的参数。
- RFC 定义了一组模幂运算群 (Modular Exponential (MODP) groups)。这意味着无需每次交换 $g$ 和 $p$,只需指定如“RFC3526 1536 MODP Group”,双方即可知道使用的参数。
- 这些标准参数避免了针对某些特定素数类的已知攻击。
- 如果 $g$ 和 $p$ 选择得当,安全性取决于随机选择的秘密 $a$ 和 $b$。
RSA 加密算法 (RSA Encryption Algorithm)
RSA (Rivest–Shamir–Adleman) 是一种非对称加密算法,也支持认证 (authentication)。密钥生成由一方完成 (例如 Alice)。
-
操作流程 (Operation):
- 密钥生成 (Key Generation): Alice 生成两个大素数 $p, q$,并计算模数 $n = pq$。
- 选择一个整数 $e$,使其与 $\phi(n) = (p-1)(q-1)$ 互素 ($\text{gcd}(e, \phi(n)) = 1$)。
- 找到整数 $d$(通常写成 $m$),使得 $e \times d \equiv 1 \pmod{\phi(n)}$。可以使用扩展欧几里得算法计算 $d = e^{-1} \pmod{\phi(n)}$。
- 公钥 (Public key) 是 $(n, e)$。
- 私钥 (Private key) 是 $(n, d)$。
- $p, q, \phi(n)$ 生成后不再需要,应保密销毁。
- 加密 (Encryption): Bob 想发送消息 $M \in Z_n^*$ 给 Alice。
- Bob 计算密文 (ciphertext) $C = M^e \pmod n$ 并发送给 Alice。
- 解密 (Decryption): Alice 接收到密文 $C$。 * Alice 计算 $C^d \pmod n$ 来恢复消息。 $(M^e)^d \equiv M^{ed} \pmod n$。由于 $ed \equiv 1 \pmod{\phi(n)}$,根据欧拉定理,$M^{ed} \equiv M^1 \equiv M \pmod n$。她成功恢复了 Bob 的消息。
- 密钥生成 (Key Generation): Alice 生成两个大素数 $p, q$,并计算模数 $n = pq$。
-
示例 (Example):
- Alice 生成密钥:选择素数 $p=11, q=17$,计算 $n = pq = 11 \times 17 = 187$。
- 计算 $\phi(n) = (p-1)(q-1) = (11-1)(17-1) = 10 \times 16 = 160$。
- 选择 $e=7$,与 160 互素。
- 找到 $d$ 使得 $ed \equiv 1 \pmod{160}$。 $7 \times d \equiv 1 \pmod{160}$。计算得 $d=23$ ($7 \times 23 = 161 \equiv 1 \pmod{160}$)。
- 公钥:$(n, e) = (187, 7)$。私钥:$(n, d) = (187, 23)$。
- Bob 发送消息 $M = 142$ 给 Alice。
- Bob 计算密文 $C = M^e \pmod n = 142^7 \pmod{187}$。计算得 $142^7 \equiv 65 \pmod{187}$。Bob 发送 65 给 Alice。
- Alice 收到 65,计算 $C^d \pmod n = 65^{23} \pmod{187}$。计算得 $65^{23} \equiv 142 \pmod{187}$。Alice 恢复了消息 142。
-
RSA 的安全性 (Security of RSA):
- RSA 问题 (The RSA problem):仅凭密文 $C \equiv M^e \pmod n$ 和公钥 $(n, e)$ 很难恢复消息 $M$ (即计算模 $n$ 的 $e$ 次方根)。目前已知最有效的方法是分解 $n$ 为 $p$ 和 $q$。
- 整数因数分解 (Integer Factorisation):给定合数 $n$,将其分解为质因数 $p_1, p_2, \dots, p_k$。目前没有已知的多项式时间算法 (polynomial time algorithm)。
- RSA 的安全性没有形式上证明是“困难”的。就像 DH 的 DLP 和 DHP 一样,我们假设 RSA 问题和整数因数分解问题在计算上是“困难”的。
- 量子算法 (Quantum algorithms):已经存在可以轻易破解 RSA 的量子算法。
-
因数分解攻击 (Factoring Attack on RSA):
- 仅凭公钥 $(n, e)$ 计算 RSA 解密指数 $d$ 的问题,与分解 $n$ 的问题,在计算上是等价的 (computationally equivalent)。
- 如果攻击者能够分解 $n$ 为 $p$ 和 $q$:
- 那么就可以计算出 $\phi(n) = (p-1)(q-1)$。
- 已知 $\phi(n)$ 和公钥 $e$,就可以计算出私钥 $d = e^{-1} \pmod{\phi(n)}$。
- 这意味着攻击者现在拥有私钥,可以解密任何消息。
- 在进行密钥生成时,选择的素数 $p$ 和 $q$ 必须使得对 $n = pq$ 的因数分解非常困难。例如,选择 $p$ 和 $q$ 的位数大致相等(但不要太接近)。
-
模数大小的演变 (Size of Modulus in RSA):
- 针对模数 $n=pq$ 的强力因数分解攻击一直在进步。
- 1977 年,发表了一个 129 位 (426 比特) 的 RSA 挑战,当时估计需要“40 万亿年”才能破解。1993 年,一个团队使用了 1600 台计算机,花了 6 个月破解。
- 1999 年,一个团队分解了 512 比特的数。
- 2009 年,RSA-768 (768 比特) 在 2 年内被分解。
- 2012 年,一个 1061 位 (320 位) 的特殊数被分解(特殊情况)。
- 这得益于计算机算力提升、算法映射优化和缓存利用提升。
- 因数分解的进展比经典密码学蛮力攻击的进展要快得多。
- 当前的建议:推荐使用 4096 位密钥,或至少 2048 位。$p$ 和 $q$ 的位数应大致相同(但不要太接近)。
对称加密与非对称加密 (Symmetric and Asymmetric Encryption)
对称加密 (Symmetric Encryption)
- 优点 (Advantages):
- 可以设计具有高吞吐率 (high throughput rates) 的算法。
- 密钥相对较短(128, …, 256 比特)。
- 可以用作构建其他构造(如 PRNGs)的基本单元。
- 可以用简单的代换和置换构建更强的密码。
- 所有已知攻击都涉及“穷举”密钥搜索 (exhaustive key search)。
- 缺点 (Disadvantages):
- 在双方通信中,密钥必须在两端都保密。
- 最佳实践要求密钥频繁更换(例如,每个会话)。
- 在大型网络中,需要 $n^2$ 数量级的密钥,这对密钥管理造成巨大问题。
非对称加密 (Asymmetric Cryptography)
- 优点 (Advantages):
- 只需要保密私钥 (private key)。
- 网络上的密钥管理只需要一个功能上可信 (functionally trusted) 的第三方 (TTP)。
- 根据使用模式,公私钥对可以长期使用(上限取决于摩尔定律等技术发展)。
- 在大型网络中,只需要 $n$ 数量级的密钥(每个参与方一个公私钥对)。
- 缺点 (Disadvantages):
- 吞吐率通常非常慢 (very slow)。
- 密钥大小通常大得多(1024, …, 4096 比特)。
- 安全性基于少数数论难题的假定困难性;所有已知难题都存在捷径攻击 (short-cut attacks)(例如,知道 $n$ 的质因数分解)。
- 公钥密码学在公共领域的使用历史不如对称密码学悠久。
组合使用 (Combining Cryptosystems)
- 对称加密和非对称加密是互补的 (complementary)。
- 非对称加密可以用于建立会话密钥 (session key),用于后续更快的对称加密通信。
- Alice 和 Bob 可以利用公钥密码学的长期优势,将公钥发布到目录中。
- 非对称加密适用于密钥管理 (key management) 和数字签名 (signatures)。
- 对称加密适用于数据加密 (encryption) 和部分数据完整性 (data integrity) 应用。
密钥长度考虑 (Considerations for Key Sizes)
- 对称密码的安全性取决于:算法强度和密钥长度。假设算法完美,则蛮力攻击是最佳攻击。
- 非对称密码的安全性依赖于数论难题的困难性。
重要概念与考点提示 (Key Concepts and Exam Tips)
以下是可能成为考点的知识点和可能的考题形式:
- 密钥交换的基本定义:密钥建立 和 密钥管理 的定义和区别。
- 对称密钥网络所需的密钥数量:计算 在 $n$ 个参与方之间进行安全通信所需的对称密钥数量。例如,Alice, Bob, Carol 和 Dave 四个参与方需要多少密钥?。
- 简单 KDC:理解其 工作流程 和 问题(单点故障、无认证、可伸缩性差、慢)。
- Merkle 谜题:理解其 工作流程。理解 攻击原理(Eve 需要破解多少谜题?复杂度是多少?与 Alice/Bob 的计算量对比)。知道其 主要缺点(大量带宽)。
- Diffie-Hellman (DH) 密钥交换:
- 理解其 核心思想。
- 能够 描述 DH 协议的步骤。
- 理解 DH 的 安全性基础 是 离散对数问题 (DLP) 和 Diffie-Hellman 问题 (DHP) 的困难性。理解 DLP 蕴含 DHP。
- 了解针对 DLP 的 经典攻击方法(穷举、Baby-step giant-step、Pollard’s rho、Pohlig-Hellman)和 量子攻击(Shor’s Algorithm)。
- 理解 参数 $p$ 和 $g$ 的作用。知道推荐使用 RFC 标准参数。
- 理解 共享秘密 $g^{ab}$ 不能直接作为密钥 的原因。
- RSA 加密算法:
- 理解其 工作流程(密钥生成、加密、解密)。
- 能够 解释 RSA 的安全性基础 是 整数因数分解问题 的困难性。
- 理解 因数分解攻击 如何破解 RSA(通过分解 $n$ 计算出 $\phi(n)$,再计算私钥 $d$)。知道计算 $d$ 和分解 $n$ 在计算上等价。
- 了解 推荐的密钥大小(例如 2048 或 4096 位)。理解模数大小随着计算能力提升而增加的趋势。
- RSA 问题 的定义。
- 数论基础:
- 理解 模运算。
- 理解 乘法群 $Z_n^*$ 的概念及其与 $Z_n$ 的区别(互素)。
- 理解 欧拉函数 $\phi(n)$ 的概念和 计算方法(尤其是当 $n=pq$ 时)。
- 理解 生成元 (generator) 的概念。知道当 $n$ 是素数时生成元总是存在。
- 理解 逆元 (inverse) 的概念。知道如何在 $Z_n^*$ 中计算逆元,特别是利用 欧拉定理 $a^{-1} \equiv a^{\phi(n)-1} \pmod n$ 或 裴蜀等式 / 扩展欧几里得算法。
- 对称加密与非对称加密对比:
- 比较 两者的 优点和缺点(吞吐率、密钥长度、密钥管理、安全性基础)。
- 理解 如何在实践中结合使用 两者(非对称用于密钥交换,对称用于数据加密)。
- 密钥长度的考虑。
示例考题 (Example Questions)
- 简述密钥建立 (Key Establishment) 和密钥管理 (Key Management) 的区别。
- 参考答案:密钥建立是指各方获得共享密钥的过程,而密钥管理是一整套支持密钥建立和维护(包括更新)密钥关系的机制和流程。
- 请说明简单密钥分发中心 (Naïve KDC) 协议的工作原理,并列举其至少三个主要问题。
- 参考答案:工作原理:Alice 向 KDC 请求与 Bob 通话,KDC 生成会话密钥,用 Alice 和 Bob 各自与 KDC 的密钥加密后发给 Alice,Alice 再将给 Bob 的部分转交给 Bob,双方解密获得会话密钥。问题:单点故障、无认证、可伸缩性差、速度慢。
- Merkle 谜题是如何让 Alice 和 Bob 在没有第三方的情况下建立共享密钥的?攻击者 Eve 破解 Merkle 谜题的计算量大概是多少(相对于 Alice 和 Bob 的计算量)?
- 参考答案:Alice 创建大量使用弱密钥加密的谜题,每个谜题包含一个强密钥和标识符,将所有谜题发给 Bob。Bob 随机选一个谜题,暴力破解弱密钥得到强密钥和标识符,将标识符发回给 Alice。Alice 根据标识符找到对应的强密钥。攻击者 Eve 平均需要破解一半的谜题,计算量约为 Alice 和 Bob 各自计算量的平方($2^{19} \times 2^{19} = 2^{38}$ 对比 $2^{19}$),所以对 Eve 更困难。
- 请描述 Diffie-Hellman 密钥交换协议的五个主要步骤,并解释其安全性基于什么数学难题。
- 参考答案:步骤:1. 协商大素数 $p$ 和生成元 $g$;2. Alice 选秘密 $a$,发 $g^a \pmod p$;3. Bob 选秘密 $b$,发 $g^b \pmod p$;4. Alice 计算 $(g^b)^a \pmod p$;5. Bob 计算 $(g^a)^b \pmod p$。安全性基于离散对数问题 (DLP) 和 Diffie-Hellman 问题 (DHP) 的困难性。
- Diffie-Hellman 问题 (DHP) 和离散对数问题 (DLP) 是什么?它们之间有什么关系?
- 参考答案:DLP:已知 $g, g^a \pmod p$,求 $a$。DHP:已知 $g^a \pmod p, g^b \pmod p$,求 $g^{ab} \pmod p$。如果能解决 DLP 就能解决 DHP,但反之不一定。
- 解释如何在 $Z_n^*$ 中计算一个元素 $a$ 的逆元 $a^{-1}$。请给出利用欧拉函数和裴蜀等式/扩展欧几里得算法的两种方法。
- 参考答案:逆元 $a^{-1}$ 满足 $a \cdot a^{-1} \equiv 1 \pmod n$。
- 欧拉函数法:计算 $\phi(n)$,则 $a^{-1} \equiv a^{\phi(n)-1} \pmod n$。
- 裴蜀等式/扩展欧几里得算法法:由于 $a \in Z_n^*$,$\text{gcd}(a, n) = 1$。利用扩展欧几里得算法找到整数 $s, t$ 使得 $sa + tn = \text{gcd}(a, n) = 1$。取模 $n$,得 $sa \equiv 1 \pmod n$,故 $s$ 是 $a$ 的逆元。
- 参考答案:逆元 $a^{-1}$ 满足 $a \cdot a^{-1} \equiv 1 \pmod n$。
- 如果模数 $n = pq$,其中 $p, q$ 是不同的素数,如何计算 $\phi(n)$?
- 参考答案:$\phi(n) = \phi(pq) = \phi(p)\phi(q) = (p-1)(q-1)$。
- 简述 RSA 密钥生成、加密和解密的过程。RSA 的安全性主要依赖于什么数学难题?
- 参考答案:密钥生成:选大素数 $p, q$,计算 $n=pq, \phi(n)=(p-1)(q-1)$;选 $e$ 与 $\phi(n)$ 互素;计算 $d$ 使得 $ed \equiv 1 \pmod{\phi(n)}$;公钥 $(n, e)$,私钥 $(n, d)$。加密:Bob 计算 $C = M^e \pmod n$。解密:Alice 计算 $M = C^d \pmod n$。安全性主要依赖于大整数因数分解的困难性。
- 解释为什么成功分解 RSA 模数 $n$ 可以破解 RSA 密码。
- 参考答案:如果能分解 $n$ 为 $p$ 和 $q$,就可以计算出 $\phi(n) = (p-1)(q-1)$。已知公钥 $e$ 和 $\phi(n)$,就可以计算出私钥 $d = e^{-1} \pmod{\phi(n)}$。拥有私钥 $d$ 就可以解密任何密文。
- 比较对称加密和非对称加密在吞吐率、密钥长度、密钥管理和安全性基础方面的区别。实际应用中通常如何结合使用它们?
- 参考答案:吞吐率:对称通常快,非对称通常慢。密钥长度:对称短(如 128-256 位),非对称长(如 1024-4096 位)。密钥管理:对称在大型网络中需要大量密钥 ($O(n^2)$),非对称只需要 $O(n)$ 个公私钥对,且只需管理私钥。安全性基础:对称依赖于算法强度和密钥长度的蛮力抵抗,非对称依赖于特定数论难题(如因数分解、离散对数)的困难性。结合使用:通常用非对称加密来安全地交换或传输对称加密的会话密钥,然后使用对称加密进行实际的数据加密传输,以利用对称加密的高效率。